因为最近读完了《Programming Massively Parallel Processors: A Hands-on Approach (4th Edition)》这本书(下面简称 PMPP),非常想结合书中的内容实操一下。
所以我结合了 cuda 入门的正确姿势:how-to-optimize-gemm 和 How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog 这两篇非常好的文章,自己结合 PMPP 中的经验写了一版代码,同时记录一下学习的过程。
第一版实现:naive
第一版基本是最 naive 的实现。如果这个矩阵乘法是 $A \times B = C$,$A$、$B$、$C$ 三个矩阵的维度分别为 $m \times k$、$k \times n$、$m \times n$,则下面的 kernel 中每个线程对应矩阵 $C$ 中的一个元素,所以每个线程会进行 $k$ 次浮点数乘加。
| |
因为是第一版实现,所以没有在乎任何的参数设置(如 block 大小等)。同时说一下下面所有的测试中都使用 float 类型计算,并用我自己的 NVIDIA RTX 3090 来测试。这一版的性能可以达到大约 2.2 TFLOPS(根据参数该卡的理论性能为 35.58 TFLOPS)。
并且注意到,这里的写法已经进行了 global memory 的 coalesced access。
第二版实现:block tiling
第二版使用了 PMPP 第 5.4 和 5.5 节中提到的 tiling 方法,即将会被重复使用的数据放置在 block 的 shared memory 中,这样减少了 global memory 的重复传输。这个思想也是对应原 repo 中的 MMult_cuda_3.cu。
| |
这里的写法大部分是直接用了 PMPP 书中 kernel 的写法。这一版可以达到大概 2.9 TFLOPS(小小进步)。
我们这里可以简单计算一下,每个线程的访存(只考虑读)次数:
- GMEM:K / kTileWidth * 2 loads,代入数值(kTileWidth = 16)得到 K / 8 loads
- SMEM:K * 2 loads
这里因为每个线程输出一个结果元素,所以每个结果元素的访存次数和每个线程的访存次数是相等的。
第三版实现:thread coarsening
这一版就比较有意思了,我们先来说一下应用的优化手法。手法是 PMPP 第 6.3 节中提到的 thread coarsening,即增加每个线程的颗粒度,不要使一个线程只负责一个元素。因为这种很细的颗粒度会导致很多的线程,所以会导致很多的 block。而当 block 或线程数很多的时候,在 GPU 中 block 之间会开始串行执行,这就增加了运行的 overhead。
还是拿我的 RTX 3090 举例,当我们设置三个矩阵都是 $1024 \times 1024$ 的方阵时,如果我们用最细颗粒度和 $16 \times 16 = 256$ 的 block 大小(随意定的),那么我们会有 4096 个 block。
然而查表可知,RTX 3090 每个 SM 最多支持 1536 个线程,16 个 block。因为我们的 block 大小是 256 个线程,所以由于每个 SM 上最大线程数(1536)的限制,一个 SM 只会分到 $1536 \div 256 = 6$ 个 block。而 RTX 3090 一共只有 82 个 SM,所以总共的 4096 个 block 需要 $4096 \div 6 \div 82 \approx 8.33$ 轮。这个轮在官方语言中称为 waves。在使用 Nsight Compute 进行 profiling 时,我们能看到这样一个属性就是“Waves per SM”,它的值也确实是我们计算的 8.33。
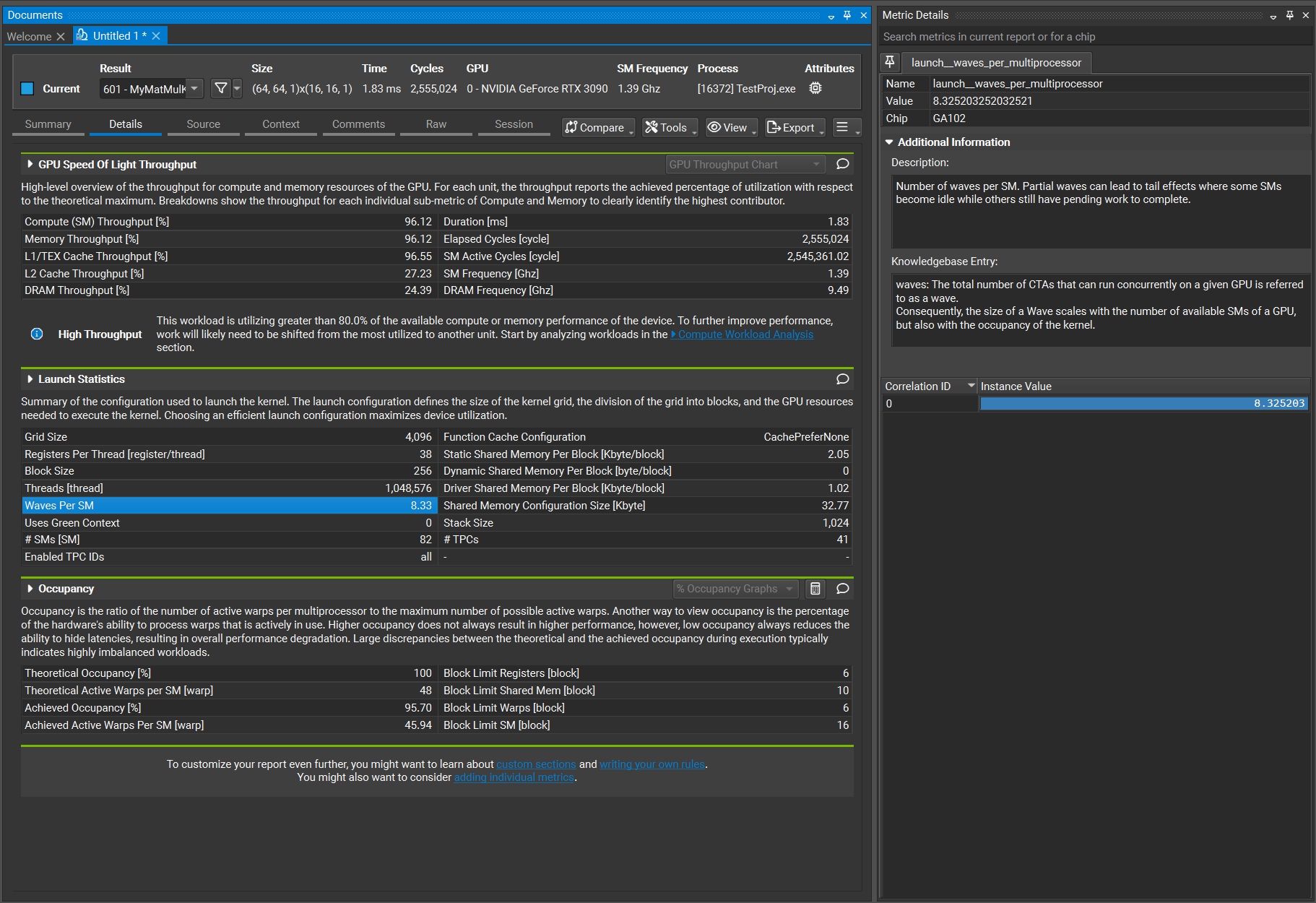
可以想象这每一轮都会有并行计算的一些 overhead(如 block 的调度开销等),所以我们可以让一个线程多处理几个元素,从而减小 block 的大小,同时也减小了总线程数。这是我们的第三版实现,在第二版上增加了一个 stride 选项,控制一个线程会计算多少个元素。
| |
在这份代码里,为了不显著地增加每个 block 的 shared memory 用量,我们将每个 block 实际负责的 tile 大小依然定为 $16 \times 16$,而 kStrideY 被用来控制每个线程负责的元素数量,从而控制了 block 中的线程大小。注意到每个 block 的大小现在是 kTileWidthX * kTileWidthY。而为了保证 tile 大小仍是 $16 \times 16$,我们要人为地保证 kTileWidthY * kStrideY = 16。所以显而易见地,如果我们将 kStrideY 设为 1,则它会回退到第二版实现;如果我们将kStrideY 设为 2、4、8 或 16,则可以进行我们上面讲的 thread coarsening。
在这一版中,由于我进行了上面的计算,所以我发现,如果 stride 超过 2,比如 stride 为 4 时,每个 block 的大小为 64 个线程,这样每个 block 的线程就会过小,使得 SM 填不满。上面我们提到,一个 SM 中只能驻 16 个 block,所以在这种情况下只能驻 $16 \times 64 = 1024$ 个线程。这会让 occupancy 掉至 $1024 \div 1536 \approx 66.7$%。所以这里我先令 stride 为 2,测试结果可以达到大约 4.1 TFLOPS(又一个小小进步)。
分析:stride 调参
这里当然既然有 stride 这个参数,不妨试一下各个参数值的效果。我测试了四个不同的参数值结果如下:
| stride | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| 计算吞吐量(TFLOPS) | 2.9 | 4.1 | 5.1 | 6.0 | 3.8 |
| Block 线程数 | 256 | 128 | 64 | 32 | 16 |
| 理论 Occupancy | 100% | 100% | 66.67% | 33.33% | 33.33% |
| 实际 Occupancy | 95.75% | 90.90% | 59.86% | 30.29% | 29.42% |
可以发现这里很“反逻辑”的一点是随着 occupancy 变低,效率反而越来越高,直到 stride 到达 16。stride 到达 16 时,一个 block 的线程数已经低于 32 了,而 warp 是以 32 个线程为一组的,所以很显然浪费了很多效率。但是在 stride 从 1 到 8 的时候效率是不断提升的。
为了研究这个问题的原因,我搜到了一个 talk《Better Performance at Lower Occupancy》,我阅读的笔记放在这篇文章里。
在这篇 talk 里,它的 case study 就是讲的 GEMM 的 thread coarsening,可以说和我这里的第三版的修改一模一样。在分析这个原因时,该 talk 中提到一个很重要的点,就是对于 GEMM 这样的 memory-intensive 的应用,计算单元的计算吞吐量是用不完的。RTX 3090 的一个 SM 的计算吞吐量是 $35.58\text{ TFLOPS } \div 82\text{ SMs }\approx 444.3\text{ GFLOPS}$。但是可以看到,我们这里的每一次乘加,都需要访问两个浮点数。所以要跑满这个计算吞吐量,我们需要 $444.3\text{ GFLOPS } \div 2\text{ ops } \times 8\text{ B } = 1777.2\text{ GB/s }$。即使我们已经把元素整体地预先 load 到 shared memory 里面了,然而 shared memory 的带宽是 $32 \text{ banks } * 4\text{ B/bank } * 1.395\text{ GHz }= 178.56\text{ GB/s}$。很明显,shared memory 的带宽依然是瓶颈。
回到我们这个例子,我们注意到在第三版代码中的第 44 行有一个 Bds[k][tx],这个元素是会被重用的。所以这里就减少了 shared memory 的读写。
同样算一下每个线程的访存(只考虑读)次数:
- GMEM:K / kTileWidth * stride * 2 loads,代入数值(kTileWidth = 16,stride = 8)得到 K loads
- SMEM:K * (stride + 1) loads,代入数值(kTileWidth = 16,stride = 8)得到 K * 9 loads
但是一个线程现在输出 8 个元素了所以每个结果元素需要的访存量变为:
- GMEM:K / 8 loads
- SMEM:K * 9 / 8 loads
当然我们要验证一下我们的想法对不对,在 Nsight Compute 中我们还能得到下面的一些性能指标:
| stride | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| 每线程寄存器量 | 38 | 40 | 40 | 52 | 72 |
| shared memory load 语句执行量 | 83.89 M | 50.33 M | 33.55 M | 25.17 M | 41.94 M |
| FMA 利用率(% active cycle) | 10.69 | 15.66 | 20.89 | 24.09 | 26.98 |
确实如我们所预料,shared memory 的加载数量在减小,同时 FMA 单元利用率在提升。
第四版实现:2D thread coarsening
那么我们基本已经确定要进一步提升计算吞吐量,所以我们要进一步减少访存量(这里说的访存是包含 shared memory 的)。所以我们进一步加强 thread coarsening 的强度,令一个线程计算 8 * 8 个元素。所以我们抛弃第三版中的 kStride,用二维的 kThreadWorkDimX 和 kThreadWorkDimY,表示一个 thread 的工作范围。
下面的实现参考了这里的源码。
| |
这个优化的关键在于第 60-70 行。通过 2D 的 thread coarsening,原理与 1D thread coarsening 类似,但是元素的重用可以更多。可以以 (kThreadWorkDimX + kThreadWorkDimY) 次 shared memory 加载进行 (kThreadWorkDimX * kThreadWorkDimY) 次乘加计算(图示过程参考该文的 Kernel 5 部分)和该文的第 1.3 节。
这时每个线程需要的访存量(只考虑读)变为:
- GMEM:K / 8 (outer loop iters) * 2 (A+B) * 512/64 (sizeSMEM/numThreads) loads,为 K * 2 loads
- SMEM:K / 8 (outer loop iters) * 8 (kTileDimK) * (8 + 8) (kThreadWorkDimY + kThreadWorkDimX) loads,为 K * 16 loads
则每个结果元素需要的访存量(只考虑读)变为:
- GMEM:K / 32 loads
- SMEM:K / 2 loads
经过测试,这时性能已经来到了 15 TFLOPS,相比之前最高的 6 TFLOPS 可以说达到了质的飞跃。
第五版实现:vectorized memory access
这一版主要做了两个改变:
- 在数据从 GMEM 读到 SMEM 时,把 As 进行转置,这样子可以进行 SMEM 的合并读取;
- 在读写 GMEM 和 SMEM 时使用
float4,以使用向量化的指令(如lde.e.128、stg.e.128、lds.128、sts.128等)
代码如下:
| |
这一版的效率可以达到约 18 TFLOPS。
第六版实现:warp tiling
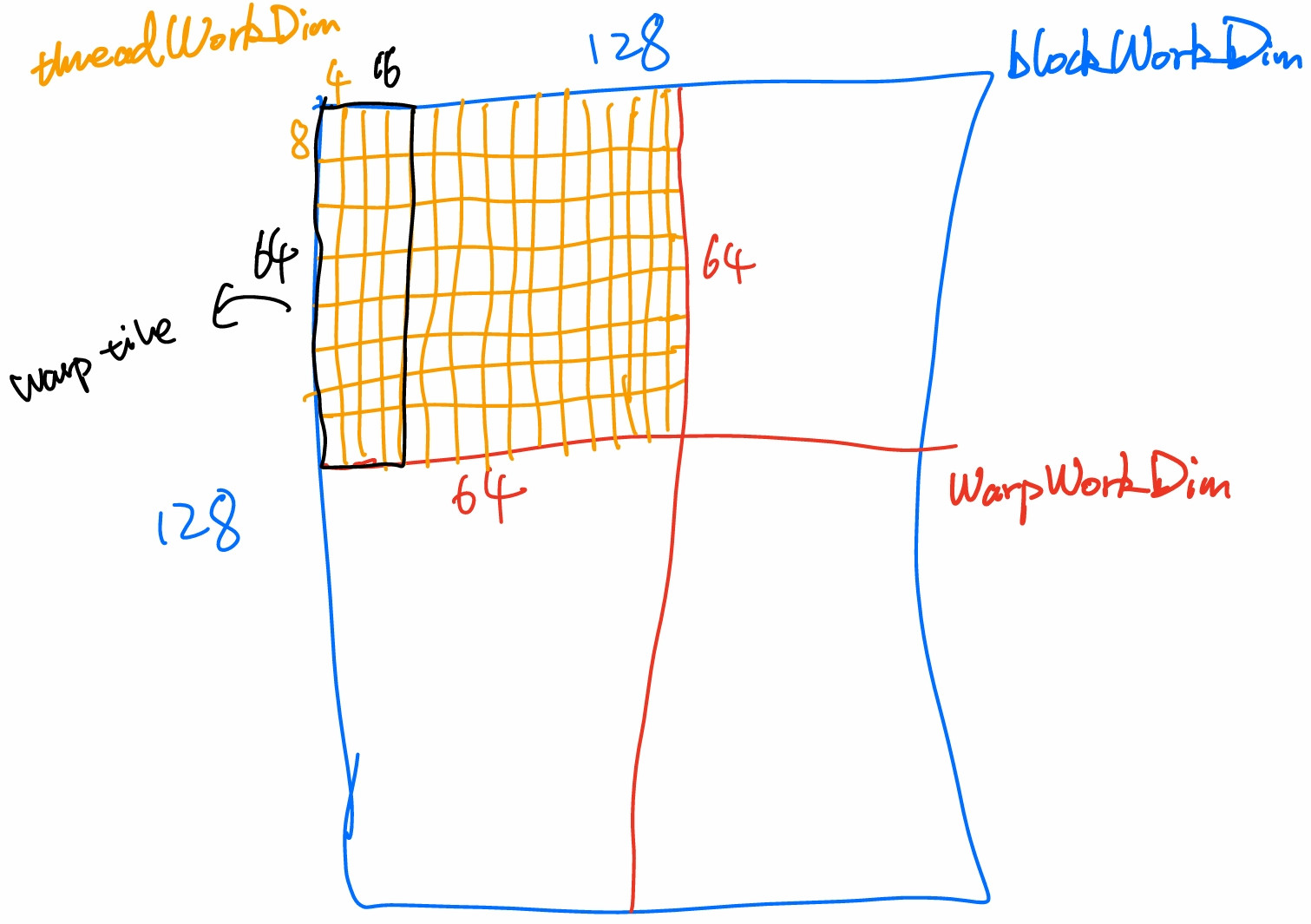
在第四版实现时我们说了,现在一个 thread tile 可以用 (kThreadWorkDimX + kThreadWorkDimY) 次 shared memory 加载进行 (kThreadWorkDimX * kThreadWorkDimY) 次乘加计算。所以很明显,在乘积确定时,kThreadWorkDimX 和 kThreadWorkDimY 越接近,算存比会越高。
那么对于一个 warp 的 32 个线程来说,这一过程是要进行 32 次的。我们可以认为每个 thread 在把数据从 SMEM 移至寄存器时,我们无形中是获得了 32 个 thread tile 在 warp 上。而这 32 个 thread tile 如果没有经过任何排布,比如是排成一行,那么可以想象,就和一个排成一行的 thread tile 一样,并没有最大化算存比。
所以通过使用 warp tile,即把 warp 也做类似的 coarsening,我们能做到的一个重要的事情是,我们可以手动控制这个 warp 的 thread tile 的分布。所以我们可以通过控制维度来让 warp 内 thread tile 的排列变成尽可能方形的,来最大化算存比。
同时我们注意到,在 kThreadWorkDimX = kThreadWorkDimY 时,这个值越大,算存比就越大。所以这样做给我们带来的另一个好处是,我们变相获得了一个很大的 thread tile。
代码如下:
| |
这一版的效率可以大概达到 20TFLOPS。
第七版实现:函数化封装
为了接来下 double buffer 的实现,我们先把现在这一版实现做一下函数封装。代码如下(只包含 kernel 部分,因为调用部分不变):
| |
第八版实现:double buffer
这一版主要是引入了 double buffer,即让 GMEM -> SMEM 和 SMEM -> REG -> 计算 这两个部分可以流水线执行。先看代码:
| |
我们可以看到,最大的区别是,从 GMEM -> SMEM 这一部分是换成了 memcpy_async(),这样不会堵塞后面的执行,并且依靠 cuda::barrier 来执行同步。可以看到两块 shared memory 分别加载两块 GMEM,并依赖于不同的 barrier,这样可以让不同块的 shared memory 分别进行“读 GMEM”和“到 REG 计算”这两个过程。