CUDA shared memory bank conflict 是会造成 shared memory 访问延迟的一个原因。这篇主要介绍两种消除 CUDA bank confict 的方法,分别为 memory padding 与 swizzling。
我们以矩阵转置为例,如果我们设定 block 的大小为 $32 \times 32$,每个 block 对 GMEM 中这个矩阵 $32 \times 32$ 的一小块进行转置。则这个 block 中的线程需要集体从 GMEM 中将矩阵搬运至 SMEM(不转置的搬运),并在转置后存储到 GMEM。注意在 SMEM 中,矩阵是没有转置的。所以在后面存储至 GMEM 时,我们需要一次读取 SMEM 中的一列数据,写入 GMEM 的一行中。
可以看到这一过程在 shared memory 中会有很强的 bank confict,因为在转置后,所有的线程都在读同一列,而这里因为大小是 $32 \times 32$,所以这一列都是同一个 bank。那么问题的根源就是破除掉这个整除的关系,即所有的线程因为整除的关系,全部被分配到了同一个 bank 进行读写。其中第一个方案是从分配空间的角度去考虑,即 memory padding。
Memory padding
Memory padding 是很简单地在开辟 shared memory 空间时,多开辟一个空间,如本来的代码为:
1
| __shared__ T shm[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_X];
|
可以改为
1
| __shared__ T shm[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_X + 1];
|
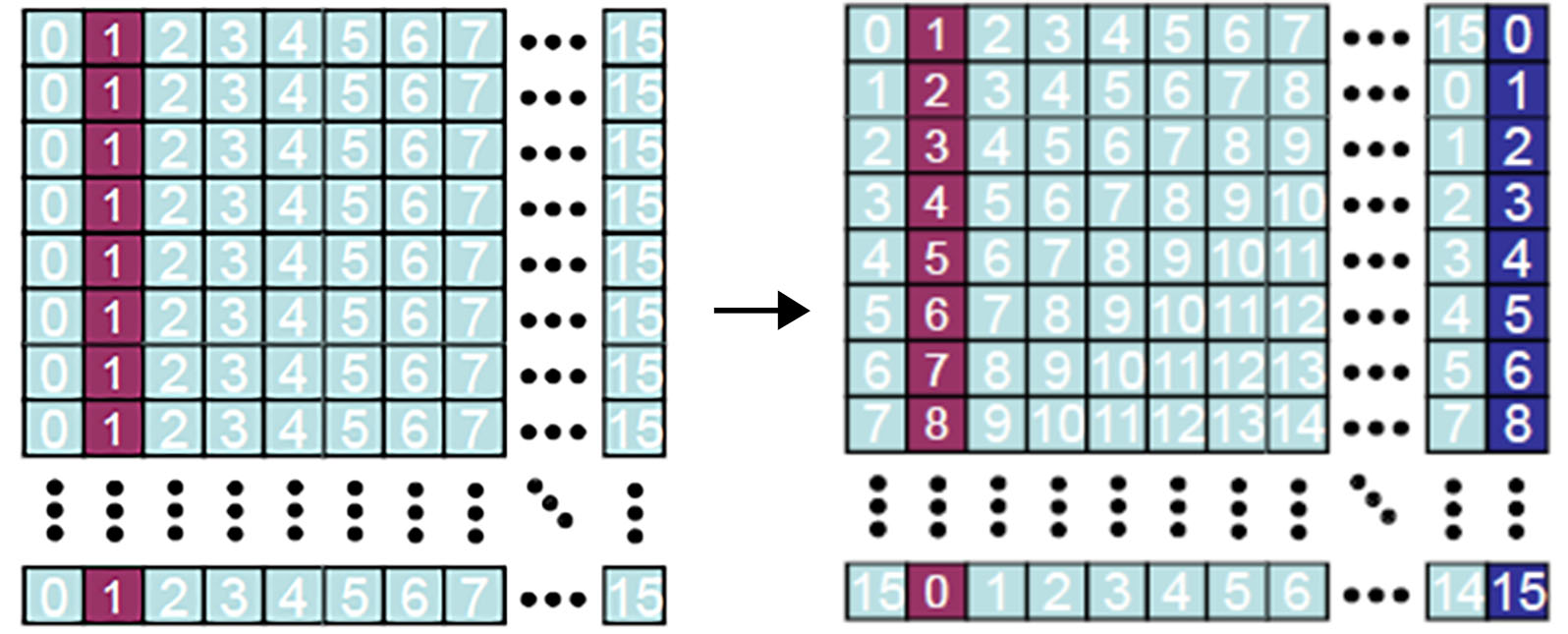
这样做可以令我们维持原有的序号进行访问,并错开实际的存储 bank。原理如下图:
Swizzling
Swizzling 的本质是改变线程到 shared memory 的索引,使得 bank 访问错开。比如对于我们上面的从 GMEM 读到 SMEM 的操作,我们可能是直接使用 threadIdx.y 和 threadIdx.x 来作为 shared memory 的索引的:
1
2
3
4
5
6
7
8
| size_t const input_matrix_from_idx_x{threadIdx.x + blockIdx.x * blockDim.x};
size_t const input_matrix_from_idx_y{threadIdx.y + blockIdx.y * blockDim.y};
size_t const input_matrix_from_idx{input_matrix_from_idx_x + input_matrix_from_idx_y * N};
size_t const shm_to_idx_x{threadIdx.x};
size_t const shm_to_idx_y{threadIdx.y};
shm[shm_to_idx_y][shm_to_idx_x] = input_matrix[input_matrix_from_idx];
|
这样一列数据就都存到了 bank 0 中。然而我们可以使用一个异或来进行错开:
1
2
3
4
5
6
7
8
9
| size_t const input_matrix_from_idx_x{threadIdx.x + blockIdx.x * blockDim.x};
size_t const input_matrix_from_idx_y{threadIdx.y + blockIdx.y * blockDim.y};
size_t const input_matrix_from_idx{input_matrix_from_idx_x + input_matrix_from_idx_y * N};
size_t const shm_to_idx_x{threadIdx.x};
size_t const shm_to_idx_y{threadIdx.y};
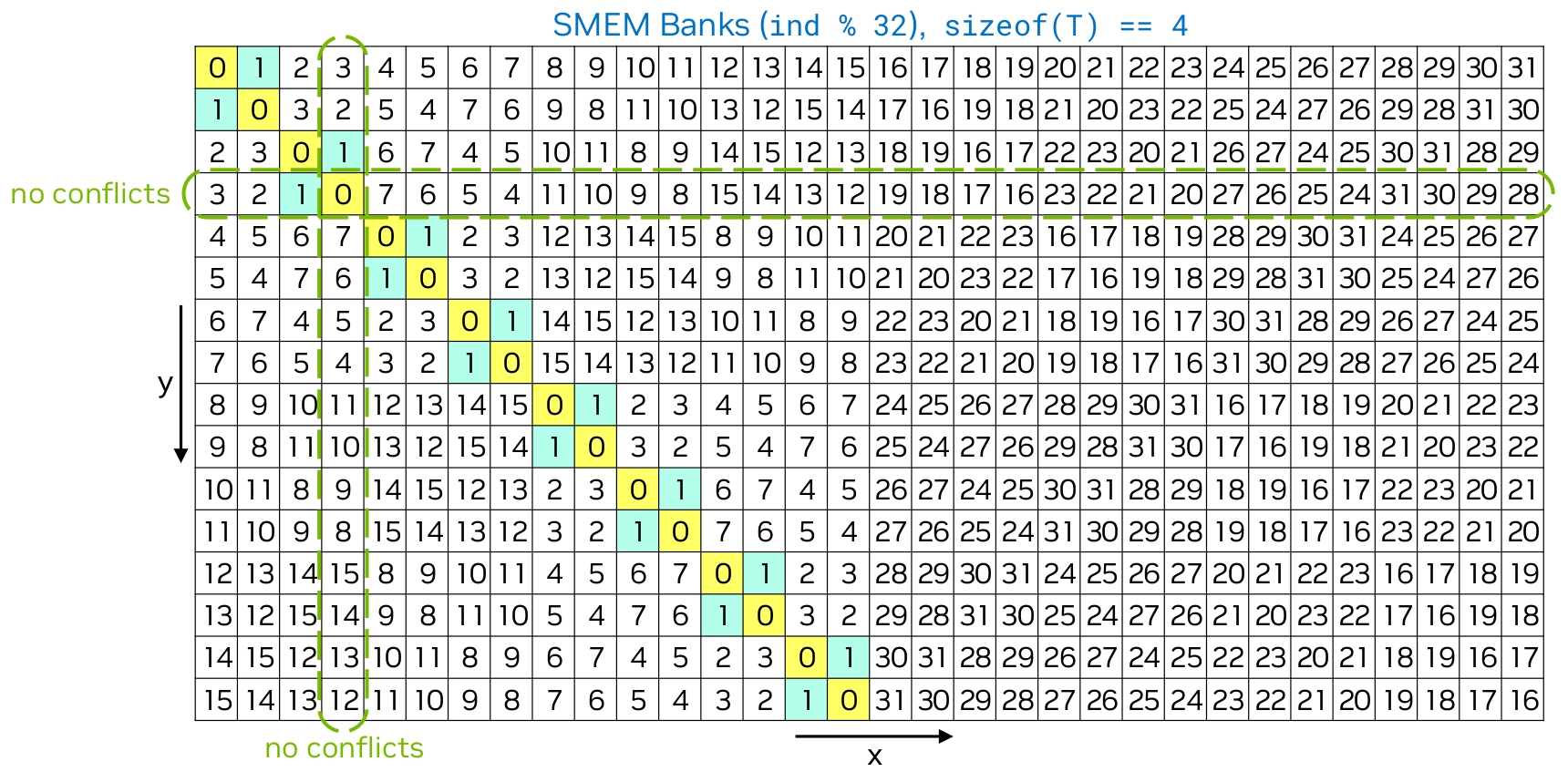
size_t const shm_to_idx_x_swizzled{(shm_to_idx_x ^ shm_to_idx_y) % BLOCK_TILE_SIZE_X};
shm[shm_to_idx_y][shm_to_idx_x_swizzled] = input_matrix[input_matrix_from_idx];
|
下图中每个方块中的数字就是 shm_to_idx_x_swizzled,也就是存储时的列号。可以看到,原本的第 0 列被存成了对角线,这样子我们再从 SMEM 中读出第 0 列时,我们会进行一个对角线读取,最小化 bank conflict(这个性质的证明在这里)。对其他列也是同理。